データ分析関連のまとめ

データ分析・機械学習周りのもくもく会LTやイベント参加をまとめていきます

Deep State Space Models for Time Series Forecasting

論文

Deep State Space Models for Time Series Forecastingを読んでまとめました。
解釈間違い等ある時がありますので、その場合指摘いただけると助かります。

目次

概要

  • 状態空間モデルとディープラーニングを組み合わせた確率的時系列予測。
  • 状態空間モデルに必要なデータの効率性や解釈性を維持しながら、深層学習により複雑なパターンを学習する。
    • 共変量から状態空間モデルパラメータへのマッピングにRNN(LSTM)が使われている。
  • 少ない学習データへの構造的仮定を組み込んだ対応から、大規模な時系列データから複雑なパターンを学習する事まで適用可能。

問題定義

  • 確率予測問題を以下と定義
  • N:一変量時系列集合とする。
 N:一変量時系列集合とする(\{ z_{1:T_i}^{(i)}   \}_{i=1}^N) 
  (z_{1:T_i}^{(i)} = (z_1^{(i)}, z_2^{(i)}, ..., z_{T_i}^{(i)})\ and\ z_t^{(i)} \in \mathbb{R} ) 
 \{ x_{1:T_i+\tau}^{(i)}\}_{i=1}^N and x_t^{(i)} \in \mathbb{R}^D: 関連する共変量ベクトル(時間変化有)

この問題で解きたいのは、将来の軌道確率分布であり、以下で表される。

 p(z_{T_i+1:T_i+\tau}^{(i)}|z_{1:T_i}^{(i)} , x_{1:T_i+\tau}^{(i)}; \Phi)
 1~T_i+\tau:\ training\ range \ T_i+1~T_i+\tau:\ prediction\ range
 \Phi : モデルの学習可能なパラメータの集合

State Space Models

方程式

  • 線形の状態遷移方程式となるモデルを考えると以下の式となる。
 \textit{l}_t = \textit{F}_t \textit{l}_{t-1} + \textit{g}_t{\epsilon}_t \ ({\epsilon}_t \sim
 N(0,1))
  • また、一変量ガウス状態空間モデルとすると、以下となる
 z_t = y_t + {\sigma}_t {\epsilon}_t \ ({\epsilon}_t \sim
 N(0,1))
 y_t = \textit{a}_t^T \textit{l}_{t-1} + b_t 
 \textit{l}_0 \sim N({\mu}_0, diag({\sigma}_0^2))

Parameter learning

  • 状態空間モデルは、パラメータで完全に指定される。
  • この論文では一般的なパラメータの推定方法として周辺尤度の最大化があげられている。
 パラメータ: {\Theta}_t = ({\mu}_0, {\Sigma}_0, \textit{F}_t, \textit{g}_t, \textit{a}_t, \textit{b}_t, {\sigma}_t)
 {\Theta}_{1:T}^* = argmax_{{\Theta}_{1:T}}pss(z_{1:T}|{\Theta}_{1:T})
 pss(z_{1:T}|{\Theta}_{1:T}) = p(z_1|{\Theta}_1) \prod_{t=2}^{T}p(z_t|z_{1:t-1}, \Theta_{1:T}) = \int p(\textit{l}_0) [ \prod_{t=1}^{T}p(z_t|\textit{l}_t)p(\textit{l}_t|\textit{l}_{t-1})]

Deep State Space Models

学習

  • 本アルゴリズムでは、各時系列毎に独立した状態空間パラメータ {\Theta}^{(i)} を学習するのではなく、以下のmappingを学習する。
 共変量(\textit{x}_{1:t}^{(i)})から状態空間モデルパラメータへのマッピングにRNN(LSTM)を使う
 {\Theta}_t^{(i)} = \Psi(\textit{x}_{1:t}^{(i)}, \Phi) \ \ \ (i=1,...,N, \ t = 1,...,T_i+\tau) 
 RNNはrecurrent\ function \ \textit{h}を介して特徴の表現を計算
 \textit{h}_t^{(i)} = h (\textit{h}_{t-1}^{(i)}), \textit{x}_t^i, \Phi
 LSTMの出力層で状態空間モデルのパラメータ{\Theta}_t^{(i)}に変換(ここが具体的にどうなっているのかはわからない...)

 データ z_{t_i}は上記パラメータを含む次の式に従った分布となる
 p(z_{1:T_i}^{(i)} | \textit{x}_{1:T_i}^{(i)}, \Phi) =pss(z_{1:T_i}^{(i)}|{\Theta}_{1:T_i}^{(i)})

また、パラメータ \Phiは以下の対数尤度関数を最大化する条件で推定される

 {\Phi}^* = argmax_{\Phi} \textit{L}(\Phi)
 \textit{L}(\Phi) = \sum_{i=1}^{N} log\textit{p}(z_{1:T_i}^{(i)} | x_{1:T_i}^{(i)}, \Phi) =  \sum_{i=1}^{N} log\textit{pss}(z_{1:T_i}^{(i)} | \Theta_{1:T_i}^{(i)})
  • モデルの概観は以下となる。

f:id:yhiss:20200801160243p:plain
モデル全体概要

Prediction

  • パラメータ \Phiを計算できると、与えられた時系列毎の確率的な予測(多変量ガウス分布の解析的な計算)が可能となる。
  • 実際は予測分布をK個のモンテカルロサンプルで表現した方が便利な場合が多い。
 \hat{z}_{k, T_i+1:T_i+\tau}^{(i)} \sim  p(z_{T_i+1:T_i+\tau}^{(i)} | z_{1:T_i}^{(i)}, \textit{x}_{1:T_i+\tau}, \Theta_{1:T_i+\tau})

状態空間モデルから予測サンプルを生成するために、training rangeの最後のステップTの時点での隠れ状態を推定。
その後遷移方程式と観測方程式を再帰的に使い予測サンプルを生成する。
本論文ではカルマンフィルタの模様

 隠れ状態l_T \sim p(\textit{l}_T|z_{1:T})が得られたとして、以下を再帰的に用いる
 y_{T+t} =  \textit{a}_{T+t}^T \textit{l}_{T+t-1} + b_{T+t}\ \ \ (t=1,...,\tau)
 \hat{z}_{T+t} =  y_{T+t} + {\sigma}_t {\epsilon}_t\ \ \ (t=1,...,\tau)
 \textit{l}_{T+t} \sim \textit{F}_{T+t} \textit{l}_{T+t-1} + \textit{g}_{T+t} {\varepsilon}_{T+t}

f:id:yhiss:20200802162414p:plain
学習後のカルマンフィルタアルゴリズム

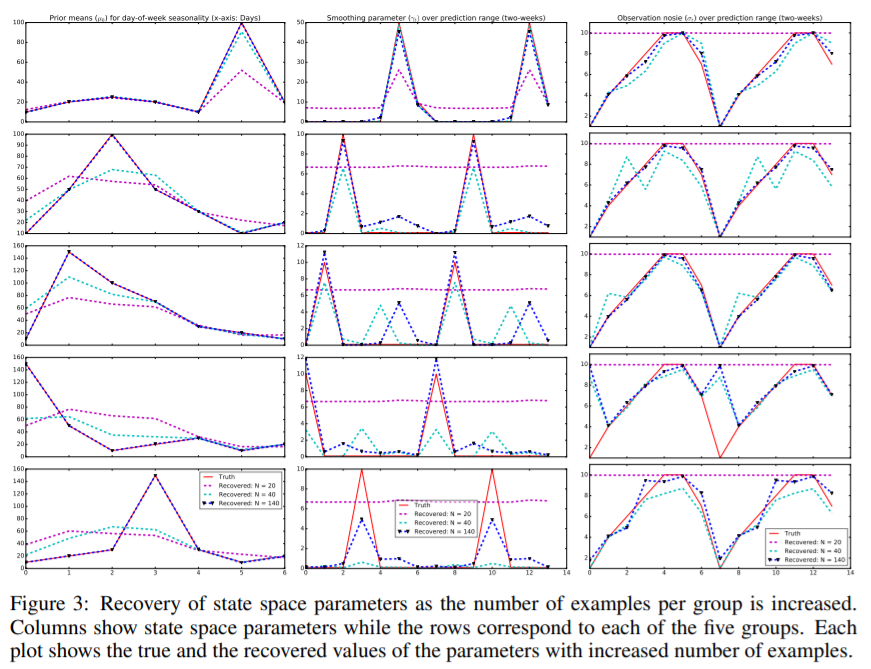
結果

  • 合成データを用いて検証する事で、データが生成された状態空間モデルのパラメータの復元が出来る事が示されている。

f:id:yhiss:20200802155450p:plain
検証結果

参考文献

https://pdfs.semanticscholar.org/7b8f/97663a190ddaf599f83d3ab6204639f8881a.pdf