データ分析関連のまとめ

データ分析・機械学習周りのもくもく会LTやイベント参加をまとめていきます

Explainable k-Means and k-Medians Clustering

論文

Explainable k-Means and k-Medians Clustering(ICML2020 Accepted paper)を読んでまとめました。
解釈間違い等ある時がありますので、その場合指摘いただけると助かります。

目次

背景と概要

  • clusteringは幾何学データの教師なし学習の代表例だが、多くのclusteringアルゴリズムはデータの全特徴量に複雑に依存するため説明が困難
  • 解釈性向上のため小さい決定木によるデータセットの分割を行った。→Explainable k-Means and k-Medians Clustering
  • 教師なし決定木:Threshold treeと本論文では読んでいる
  • アルゴリズム
    • 以下の2つの場合に分かれる。
    • k=2→Single Threshold Cut:Binary
    • k>2→IMMアルゴリズム:決定木のノードを動的計画法を用いて選択する。
  • 通常のk-means clusteringとTree based clusteringの概観が以下のように示されている。
    • 本論文では、このClusterの分割され方を以て説明性が上がったとしている。
    • 図における✖印がmistakeと定義されている。この数を最小化する事も今回のアルゴリズムに含まれている。

f:id:yhiss:20200620145050p:plain

左:通常の5-means clustering、中央:右の決定木で決定されたTree based 5-means clustering

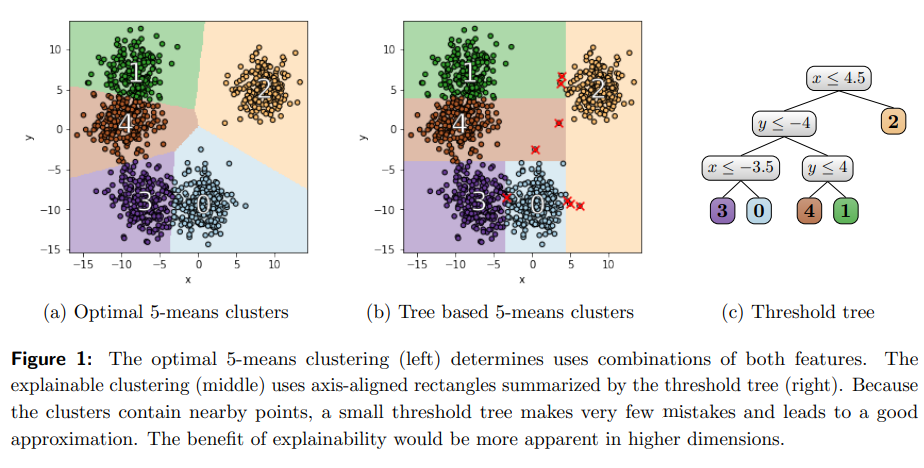
k-means、k-median clustering

  • k-meansとk-medianのゴール:与えられた集合 \chi をk個の部分集合に分割してcluster中心までの点の距離を最小化
 \chi = \{ \vec{x}^1,...,\vec{x}^n  \} \in \mathbb{R^d}

 k-meansは以下を最小化する
 {cost}_2 ( \vec{\mu}^1, ... , \vec{\mu}^k) = \sum_{\vec{x} \in \chi} || \vec{x} - c_2(\vec{x}) ||_2^2
 (argmin_{\vec{\mu} \in \{ \vec{\mu}^1, ... , \vec{\mu}^k \}} || \vec{\mu} - \vec{x} ||_2) 

 また、k-medianは以下を最小化
 {cost}_1 ( \vec{\mu}^1, ... , \vec{\mu}^k) = \sum_{\vec{x} \in \chi} || \vec{x} - c_1(\vec{x}) ||_1
 (argmin_{\vec{\mu} \in \{ \vec{\mu}^1, ... , \vec{\mu}^k \}} || \vec{\mu} - \vec{x} ||_1)

Explainable k-Means and k-Medians Clustering

  • 以下の順番で記載
    • threshold treesを使ったClustering
    • k=2の場合のSingle Threshold Cutを用いたClustering
    • k>2の場合のClustering:Iterative Mistake Minimization (IMM) algorithm

threshold treesを使ったClustering

  • 2つのclusterを定義する最も単純な方法:1つの特徴量の閾値に基づいてデータを分割する事となる(Single Threshold Cut)。
 2つのclusterは座標iと閾値\thetaを用いて \hat{C}^{\theta,i}=(\hat{C}^1,\hat{C}^2)と書ける
 1つめのcluster \hat{C}^1はx_i \leq \theta、2つめのclusster \hat{C}^2はそれ以外の場合となる
  • k>2の場合には、上記に閾値に基づいた分割(Binary Threshold Cut)を反復的に用いる。
  • これらに基づいたk個の葉をもつthreshold treeによるk-medians、k-meansのコストは以下となる。
 cost_1(T) = \sum_{j=1}^{k} \sum_{x \in \hat{C}^j} || x - median(\hat{C}^j) ||_1
 cost_2(T) = \sum_{j=1}^{k} \sum_{x \in \hat{C}^j} || x - mean(\hat{C}^j) ||_2^2

k=2の場合のSingle Threshold Cutを用いたClustering

  • 2-meansの場合を考える。
  • k=2の場合のコストは以下となる。
    • 右辺第一項:1つ目のClusterについての計算、第二項:2つ目のClusterについての計算
 cost(p) = \sum_{j=1}^{p} || \vec{x}^j - \vec{\mu}^1(p) ||_2^2 + \sum_{j=p+1}^{n} || \vec{x}^j - {\vec\mu}^2(p) ||_2^2
 \vec{\mu}^1(p)=\frac{1}{p}\sum_{j=1}^{p}\vec{x}^j, \vec{\mu}^2(p)=\frac{1}{n-p}\sum_{j=p+1}^{n}\vec{x}^j

k>2の場合のClustering:Iterative Mistake Minimization (IMM) algorithm

アルゴリズム

  • 最初のステップ:k-meansやk-mediansといったアルゴリズムによるcluster centersを参照セットとする。
    • 各データ点 x_jに最も近いcluster centersのラベル y_jを割り当てる。
  • 以下がbuild tree procedureと呼んでいる決定木の構築ステップとなる。
    • 決定木の構築:Binary splitを使用したTop-down
    • Treeの各ノードuは、そのノードで表現される入力空間(a hyper-rectangular region cell(u))と関連付けられる。
    • ノードの選択には動的計画法を用いて、特徴量 i \in dと閾値 \theta \in \mathbb{R} を適切に設定し、えられるノード内に少なくとも1つのcluster centersを含む様にする。更に最もmistakeが少ないようにする。
      • (上記cell(u)に複数の \vec{\mu}^jが含まれる場合、そのcellは分割される必要がある。)
      • mistakes:本来のclusterとは別のclusterに分けられてしまう数
  • 以下が今回のアルゴリズムを示している。

f:id:yhiss:20200620191108p:plain
IMMアルゴリズム

参考文献

arxiv.org